Escuchemos la gravedad de la Tierra.
Amarra unos pesos en una cuerda, todos a la misma distancia.
Una opción rápida puede ser...
... usar clips de papel y tuercas.
Luego toma la cuerda, suéltala y escucha la caída.
www.ciensacion.org | Los experimentos prácticos de Ciensación están publicados como Recursos Educativos Abiertos bajo la licencia internacional Creative Commons Attribution-ShareAlike 4.0 International License.
Escuchemos la gravedad de la Tierra.
Amarra unos pesos en una cuerda, todos a la misma distancia.
Una opción rápida puede ser...
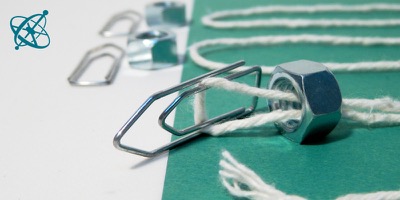
... usar clips de papel y tuercas.
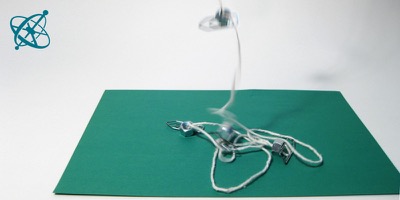
Luego toma la cuerda, suéltala y escucha la caída.
Caída libre
La fuerza de gravedad, que Newton descubrió observando la caída de una manzana, acelera todos los objetos hacia el centro de la Tierra. Con este experimento los alumnos podrán escuchar la aceleración g como un ritmo en aumento. Y, si logran modificar la configuración del dispositivo para que produzca un ritmo constante, podrán demostrar que entienden las leyes subyacentes de la física.
Escuchar la aceleración gravitatoria.
Traducir modelos matemáticos en soluciones prácticas.
Pesos que puedan amarrarse fácilmente a la cuerda
Regla
Prepara para cada grupo una cuerda de dos metros de largo y seis pesos que puedan amarrarse fácilmente a la cuerda. Las tuercas y clips de papel que se ven en las imágenes son apenas una sugerencia.
Escucha el sonido producido por los pesos cuando caen.
1. ¿Por qué el ritmo aumenta?
2. ¿A qué distancia deberías amarrar los pesos para obtener un ritmo constante?
(si es necesario)
En el momento que sueltas la cuerda, ¿cuál es la velocidad descendiente de los pesos?
› No tienen velocidad.
¿El primer y el último peso llegan al piso a la misma velocidad?
› No, el último se ha estado acelerando por más tiempo, por lo tanto llega al piso a mayor velocidad.
¿Cuán lejos cae un objeto en un determinado tiempo?
› Según las leyes de Newton podemos deducir que h = 0.5 g t2.
Si quieres que el tiempo t entre dos objetos que caen al suelo sea el mismo, ¿a qué distancia h deberían estar amarrados en la cuerda?
› La distancia aumenta con el número de cada peso elevado al cuadrado: h1 = k 12, h2 = k 22,..hn = k n2, donde k puede ser cualquier constante, por ejemplo k = 5 cm.
Los pesos aceleran su velocidad mientras caen. Por lo tanto, cada peso llega al piso a una velocidad más alta que el anterior y necesita menos tiempo para recorrer la distancia entre dos pesos. Por eso, el tiempo de llegada al piso entre dos pesos se acorta y el observador escucha que el ritmo aumenta.
Para generar un ritmo constante, lo que debe ser constante no es la distancia entre los pesos, sino el tiempo que tardan los dos pesos en llegar al piso. Como h ~ t2, la distancia tiene que aumentar con el número de cada peso elevado al cuadrado: n, es decir hn~ n2. Una posible solución es amarrar los pesos con las siguientes distancias: 5 cm, 20 cm, 45 cm, 80 cm, 125 cm y 180 cm.